量子情報科学序論 IBM Qを動かして学ぶ量子コンピュータ
【前置き】この記事は『量子コンピュータ Advent Calendar 2017』の12月16日分です. 11月の三田祭(慶應義塾大学の文化祭)にてLYNCSが配布した部誌『Escape Velocity』の記事を一部改訂(最新のニュースを反映)したものになっております.
$$ \newcommand{\bra}[1]{\left\langle #1 \right|} \newcommand{\ket}[1]{\left|#1 \right\rangle} \newcommand{\bracket}[2]{\left\langle #1 \middle|#2 \right\rangle} $$
みなさんこんばんは。いよいよ三田祭まで一週間を切りましたね!
— LYNCS(宇宙科学総合研究会)【公式】 (@keio_LYNCS) 2017年11月19日
LYNCSは今回初めて、会誌「Escape Velocity」を発行します!
三田祭当日に頒布予定です。ぜひ会場でお手にとってご覧ください! pic.twitter.com/ltVr3HIZ3Z
概要
量子計算機のアルゴリズムの基礎を学びます. 直感的理解のため, 読者が実際にIBMの保持する量子計算機をクラウド上で実行できるように導入します. 最後に少し最近のニュースに触れています.
はじめに
みなさん初めまして. LYNCS理学研究本部所属のTsujishin(@shin_tsujido)と申します. 本年度, LYNCS理学研究本部では量子情報科学の輪講を行いました. 量子情報科学は年々規模が拡大しており, 各国各企業の研究の一部は実装の段階に移行しつつあります. 一方,量子情報科学が世間から十分に理解を得られているとは言い難いです(『量子コンピュータ』の定義の議論含め). よって本誌では学部1年レベルの線形代数以外に前提知識を必要とせず, 分野に関しての一歩目となるような序論を展開します. また, 読者が量子コンピュータ(IBMQ)の操作を一通りできるような導入を行います.
量子情報科学とは
量子情報科学とは, 量子力学を物理的基盤(ハードウェア構成要素が従うことわり)としている情報科学(コンピュータ科学を含む)のことです. 具体的には, 量子コンピュータ(計算機)や量子通信, 量子暗号などに関する学問です. 80年代にベニオフやファインマン, ドイチュの構想から始まった分野ですが, 人類の不断の努力によって実用段階になりつつあります. 多くの量子情報科学におけるアルゴリズムは後述する重ね合わせや量子もつれなどの性質を用いることでより効率的な計算やより安全な通信を実現しています. 1
量子コンピュータ
ガ○ダム00やマブ○ヴオルタなどのSFでもよく目にする量子コンピュータ. それは果たしてどのようなコンピュータなのでしょうか. 理想的な計算機(コンピュータ)のモデルとしてよく語られるものにチューリングマシンがありますが, 量子コンピュータのモデルの一つである量子チューリングマシンは, 計算可能性(どんな問題を解くことができるか)は等価になっています. チューリングマシンで解くことができない問題は量子チューリングマシンでも解くことはできません. しかし, 解くことができる計算において, 計算量(計算の手順数)では, 量子チューリングマシンはチューリングマシン以下になること, すなわちより効率よく計算できる可能性があることが示されています. また, 量子チューリングマシンはチューリングマシンのエミュレート(動作の真似をすること)ができます.
量子ゲート(回路)方式計算機と呼ばれる方式は量子コンピュータで最も歴史的に研究されてきました. 量子ゲート方式は既存のコンピュータの汎用性を引き継ぎ, さらに計算を効率化することを目標としています. また, 断熱計算機や量子シミュレータなどと呼ばれる計算機がよく量子ゲート方式計算機への比較の対象として取り上げられてきました. 断熱計算機には量子アニーリング方式と呼ばれるタイプのコンピュータがあります. 量子アニーリング方式計算機は, カナダのD-Wave社が実用化し話題を呼びました. 他にもコヒーレントイジングマシン(開発者の方は量子ニューラルネットワークと呼称されています)と呼ばれる光を用いた計算機が比較対象にされることもあります. 量子アニーリング方式やコヒーレントイジングマシンは最適化問題(サラリーマン巡回問題やグループ分けの問題など. グラフ理論などに関連する問題)を解くことに特化しています. コヒーレントイジングマシンは分かりやすく基本的な仕組みが説明されている記事があるのでリンクを貼っておきます.
また, クラウドで実際に動かすこともできます.
これらさまざまな非ノイマン型計算機(特殊な計算機)のうちいくつかは, 量子力学的性質を用いることで様々な問題の計算量(計算複雑性)を減らすことを試みています. 計算量とは, 問題を解くのに当たって必要な計算の回数なので, これを減らすことによってより短い時間で計算できるようになります. 現在, 量子コンピュータ開発は規模を拡大しつつあります. アメリカ国防省は毎年約220億円投資しており, EUは2019年からの10年で1300億円, 日本も来年度予算で32億円投資予定です. 2 世界中の研究室で量子コンピュータなどの非ノイマン型計算機の開発は続いており, 以下のように様々な物質の性質を用いた非ノイマン型計算機が研究されています.
(A)ゲート方式
(B)量子アニーリング
(C)コヒーレントイジングマシン
*光(パルス) NTT, NII, Stanford
量子力学的性質
物理を古典力学から量子力学に拡張したら、計算は拡張されたんだ。それは、これまで数学的に決まっていると思っていた計算が、実は古典物理をもとに作られた計算だったからだ。そのことに我々は気づいていなかった. - David Deutsch(1953〜)3
量子力学を用いると何が今までのコンピュータ(量子情報科学者は敬意を込めて古典コンピュータと呼称する)や通信と違うのでしょうか. そもそも量子力学とは, 電子や光子(フォトン)などミクロな領域から始まった物理学です(マクロな物体における量子力学の話は長くなるので今回は割愛します).量子力学においてはマクロな世界観を持った我々の感覚とは異なる現象が多々起こります.
例えば, 量子力学では, 観測という概念が非常に重要です. 古典力学(非量子力学)では, 初期値(例えば物体の位置や速度, 加速度)がわかればその後の運動は基本的に予測できます(外部からの影響がない限り). しかしながら量子力学では, 観測するまでその後の推移は確定できません.
量子力学の最も重要な現象(概念)として, 重ね合わせと量子もつれという現象があります. 量子コンピュータでは, これらの現象を用いて量子ビットと呼ばれる情報単位を生成し, 計算を行っています.
量子ビット
古典コンピュータでは, 情報の最小単位としてビット(bit)を用います. ビットは、0もしくは1の2通りの情報を表現することができます. これをn個用意することによって, 2nの状態を表現することができます. 量子情報科学分野では, 古典ビットと呼称します. 古典ビットは, 物理的には主に電圧の高下などを用います. また, 古典ビットはコピーすることができます.
それに対し, 量子コンピュータは量子ビット(Qubit)と呼ばれる情報の単位を用います. この量子ビットは, 古典計算機のビットのように, 二つの情報を表現することができます. この時, 量子ビットでは, 二つの直行するベクトル(二次元複素ベクトル空間での正規直交基底)を用いて情報を表現します.4 また, 量子分野ではよく, ベクトルをブラッケット記法という記法で表現します.
ブラケット記法では, 任意のベクトルは,$\ket{}$(ケットと読みます)のような記号に入れて表現します.
例えば, 古典ビットにおける0と1に相当する単純な状態は,
$$ \ket{0} ≡ \left( \begin{array}{r} 1 \\ 0 \\ \end{array} \right) \ket{1} ≡ \left( \begin{array}{r} 0 \\ 1 \\ \end{array} \right) $$
のように表現されます. ケットの中に入る数字もしくはアルファベットは, 特に意味はなく, ラベルづけ(ベクトルに名前をつける)として機能します. つまり,
$$ \ket{*°Д°} ≡ \left( \begin{array}{r} 12345 \\ 54321 \\ \end{array} \right) $$
のようにケットの中には好きなものを入れてベクトルを置くことができます. なお量子力学では, 主に$ψ$(プサイ)や$φ$(ファイ)を用います. なお, 複数の量子の状態を表す時, $\ket{}$の中に複数の状態を入れることもできます. 例えば, $\ket{0}$の量子ビットが二つあった時, $\ket{00}$のように表現することができます.
この量子ビットをより視覚的に捉えるツールとして, ブロッホ球という概念があります. 球の表面は中心からの距離がどこでも等しいので, 2次元複素ベクトル空間内のあらゆる単位ベクトルを表現可能です. ブロッホ球はベクトルのZ軸で$\ket{0}$と$\ket{1}$を観測できる確率を表し、XY平面の角度で位相を表します。北極が$\ket{0}$, 南極が$\ket{1}$に相当します. 例えば,
$$\ket{ψ}=\cos\frac{θ}{2}\ket{0}+exp(iφ)\sin\frac{θ}{2}\ket{1}$$
は以下のようになります.

量子ビットは, 物理的には光子や電子のエネルギー, 原子のスピンなどで実現されます.
重ね合わせ
古典ビットにはない性質として, 量子ビットは古典ビットと違い, 0と1が共存した状態を生成することが可能になっています. この共存した状態とは, 2次元複素ベクトル空間内のあらゆる単位ベクトル(大きさ1のベクトル)を表現可能です.
$$ \ket{ψ} =a\ket{0}+b\ket{1} = \left( \begin{array}{r} a \\ b \\ \end{array} \right) $$
この式が意味するのは, 確率$|a|^2$で状態$\ket{0}$, 確率$|b|^2$で状態$\ket{1}$が観測できるという状態です. 例えば,
$$ \ket{ψ} =\frac{\ket{0}+\ket{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}}{\left( \begin{array}{r} 1 \\ 1 \\ \end{array} \right)} $$
では,それぞれ $\left( \frac{1}{\sqrt{2}} \right) ^2=\frac{1}{2}$の確率で状態$\ket{0}$, $\ket{1}$を観測できます.
このような現象を活用することで, 複数のデータ(状態)に対して同時に操作を行うことができ, 古典コンピュータへのアドバンテージになっています. 物理的にどのようなことであるのかなどより深く知りたい方は, "シュレーディンガーの猫"などに関して調べてみてください.
量子もつれ
もう一つ古典ビットと明確に違う性質として, 量子もつれがあります. これは, 複数の量子ビットにおいて発生することのある特殊な相関です. まずは簡単のため, 二つの量子における量子もつれを考えましょう. 1つ目の量子をA, 2つ目の量子をBとします. ここで2量子のもつれかつ重ね合わせの4つの状態(Bell pair)を例に出してみましょう.
$$ |\Phi^+\rangle ≡ \frac{1}{\sqrt{2}} (|0\rangle_A \otimes |0\rangle_B + |1\rangle_A \otimes |1\rangle_B) $$ $$ |\Phi^-\rangle ≡ \frac{1}{\sqrt{2}} (|0\rangle_A \otimes |0\rangle_B - |1\rangle_A \otimes |1\rangle_B) $$ $$ |\Psi^+\rangle ≡ \frac{1}{\sqrt{2}} (|0\rangle_A \otimes |1\rangle_B + |1\rangle_A \otimes |0\rangle_B)\ $$ $$ |\Psi^-\rangle ≡ \frac{1}{\sqrt{2}} (|0\rangle_A \otimes |1\rangle_B - |1\rangle_A \otimes |0\rangle_B)\ $$
例えば$|\Phi^+\rangle$では,確率$\left( \frac{1}{\sqrt{2}} \right) ^2=\frac{1}{2}$で A,B共に$\ket{0}$, 確率$\left( \frac{1}{\sqrt{2}} \right) ^2=\frac{1}{2}$でA,B共に$\ket{1}$という意味です. $|\Phi^+\rangle$では, バラバラに観測しても片方のみが0, もう片方が1,という結果は得られません. 片方の量子ビットを観測した時点で両方の状態は確定するということを意味します.
このように, 多量子系において, 複数の量子の状態が不可分になっている状態を量子もつれと呼称します. 物理的にどのようなことであるのかなどより深く知りたい方は, "EPRパラドックス", "CHSH不等式"などに関して調べてみてください.
ゲート方式量子コンピュータ
量子ゲート(回路)方式計算機では, 量子回路を用いて量子ビットを操作します. これは, 既存の計算機における電子回路の論理回路の拡張になっています. 量子回路は量子ゲート(素子)から構成されており, を量子ビットに対して掛けることを「量子素子を適用する」と呼称します. 量子ゲートは, 図のように, 線の上にボックスを乗せて表記します. この時線一本が1量子ビットを表しています.

この節では, IBMの量子計算機に実装されている量子ゲートを説明します. 量子回路は, 量子ビットから量子ビットへの変換を行い, ユニタリー行列として与えられます.

任意のユニタリー行列Uは,
$$U^{*}U=UU^{*}=I$$
となっています. ここで, $U^*$は, 行列$U$の転置(後述)かつ複素共役(実部はそのまま虚部の符号を反転すること)な行列, $I$は単位行列となっています. 転置とは, m行n列の任意の行列Aの$(i,j)$成分と$(j,i)$成分を入れ替えたn行m列の行列$A^{\mathrm{T}}$を表します.
また, 単位行列とは, 対角成分に$0$が並び, それ以外に$1$が並んだ行列のことです. つまり, 行列要素$a_ij$に関して,
$$ a_ij= \begin{cases} 1 & (i=j) \\ 0 & (i\neq j) \end{cases} $$
という式が成り立つ行列を表します.
恒等演算子
恒等演算子は以下のような行列で, どのような量子ビットに対して適用しても量子ビットの状態は変化しません. つまり, 入力と出力が等しいゲートということになります. よくIやIdと表記します.
$$ I ≡ \left( \begin{array}{rr} 1 & 0 \\ 0 & 1 \\ \end{array} \right) $$

パウリXYZゲート
パウリX
$$ X ≡ \left( \begin{array}{rr} 0 & 1 \\ 1 & 0 \\ \end{array} \right) $$
パウリXゲートは, ビット反転演算子とも呼ばれます. これは, パウリXゲートを量子ビットに適応すると, 以下のように$\ket{0}$は$\ket{1}$に, $\ket{1}$が$\ket{0}$に変換できるためです. これは古典におけるNOTゲートに相当します. また, ブロッホ球上では, $x$軸の周りに角度$π$回転させる操作と捉えることができます.
$$ X\ket{0}= \left( \begin{array}{rr} 0 & 1 \\ 1 & 0 \\ \end{array} \right) \left( \begin{array}{r} 1 \\ 0 \\ \end{array} \right) =\left( \begin{array}{r} 0 \\ 1 \\ \end{array} \right) =\ket{1} $$ $$ X\ket{1}= \left( \begin{array}{rr} 0 & 1 \\ 1 & 0 \\ \end{array} \right) \left( \begin{array}{r} 0 \\ 1 \\ \end{array} \right) = \left( \begin{array}{r} 1 \\ 0 \\ \end{array} \right)=\ket{0} $$
量子回路上では以下のように表現します.

パウリY
$$ Y ≡ \left( \begin{array}{rr} 0 & -i \\ i & 0 \\ \end{array} \right) $$
パウリYゲートは, 位相・ビット反転演算子とも呼びます. ブロッホ球上では, $y$軸の周りに角度$π$回転させる操作と捉えることができます.
$$ Y\ket{0}=\left( \begin{array}{rr} 0 & -i \\ i & 0 \\ \end{array} \right) \left( \begin{array}{r} 1 \\ 0 \\ \end{array} \right) =\left( \begin{array}{r} 0 \\ i \\ \end{array} \right) =i\ket{1} $$ $$ Y\ket{1}=\left( \begin{array}{rr} 0 & -i \\ i & 0 \\ \end{array} \right) \left( \begin{array}{r} 0 \\ 1 \\ \end{array} \right) =\left( \begin{array}{r} -i \\ 0 \\ \end{array} \right) =-i\ket{0} $$
量子回路上では以下のように表現します.

パウリZ
$$ Z ≡ \left( \begin{array}{rr} 1 & 0 \\ 0 & -1 \\ \end{array} \right) $$
パウリZゲートは, 位相反転演算子とも呼びます.ブロッホ球上では, $z$軸周りに角度$π$回転することを意味します. $\ket{0}$に対しては何も変化させず,$\ket{1}$に対しては, 状態に対しては位相のみ反転を行います.
$$ Z\ket{0}=\left( \begin{array}{rr} 1 & 0 \\ 0 & -1 \\ \end{array} \right) \left( \begin{array}{r} 1 \\ 0 \\ \end{array} \right) =\left( \begin{array}{r} 1 \\ 0 \\ \end{array} \right) =\ket{0} $$ $$ Z\ket{1}=\left( \begin{array}{rr} 1 & 0 \\ 0 & -1 \\ \end{array} \right) \left( \begin{array}{r} 0 \\ 1 \\ \end{array} \right) ] [ =\left( \begin{array}{r} 0 \\ -1 \\ \end{array} \right) =-\left( \begin{array}{r} 0 \\ 1 \\ \end{array} \right) =-\ket{1} $$
量子回路上では以下のように表現します.

アダマールゲート
$$ H ≡ \frac{1}{\sqrt{2}}\left( \begin{array}{rr} 1 & 1 \\ 1 & -1 \\ \end{array} \right) $$
アダマールゲートは, 量子ビットを重ね合わせ状態にすることができるゲートです. アダマール変換とも呼称します. アダマールゲートは, フランス人Hadamardに因んで名付けられました. フランス語で頭文字のHと最後のDは発音しないので, ハダマードではなくアダマールと呼びます.
$$ H\ket{0}=\frac{1}{\sqrt{2}}\left( \begin{array}{rr} 1 & 1 \\ 1 & -1 \\ \end{array} \right) \left( \begin{array}{r} 1 \\ 0 \\ \end{array} \right) =\frac{1}{\sqrt{2}} \left( \begin{array}{r} 1 \\ 1 \\ \end{array} \right) $$ $$ H\ket{1}=\frac{1}{\sqrt{2}}\left( \begin{array}{rr} 1 & 1 \\ 1 & -1 \\ \end{array} \right) \left( \begin{array}{r} 0 \\ 1 \\ \end{array} \right) =\frac{1}{\sqrt{2}} \left( \begin{array}{r} 1 \\ -1 \\ \end{array} \right) $$
ここで
$$ \frac{1}{\sqrt{2}} \left( \begin{array}{r} 1 \\ 1 \\ \end{array} \right)=\frac{\ket{0}+\ket{1}}{\sqrt{2}} $$
であり, これは量子ビットを観測するとそれぞれ$\left( \frac{1}{\sqrt{2}} \right) ^2=\frac{1}{2}$の確率で状態$\ket{0}$, $\ket{1}$という結果を得ることができる重ね合わせの状態です.
量子回路上では以下のように表現します.

位相シフトゲート
$$ S ≡ \left( \begin{array}{rr} 1 & 0 \\ 0 & i \\ \end{array} \right) S^\dagger ≡ \left( \begin{array}{rr} 1 & 0 \\ 0 & -i \\ \end{array} \right) $$ $$ T ≡ \left( \begin{array}{rr} 1 & 0 \\ 0 & exp(i\frac{\pi}{4}) \\ \end{array} \right) T^\dagger ≡ \left( \begin{array}{rr} 1 & 0 \\ 0 & exp(-i\frac{\pi}{4}) \\ \end{array} \right) $$
位相シフト演算は, 任意の重ね合わせ状態に対して適用すると, $\ket{0}$には何も操作を行わず, $\ket{1}$にのみ位相の操作を行います. 将来的には位相の角度を指定して様々な位相シフトゲートを作ることができることが望まれていますが, 今回操作する予定のIBM Qでは二つの角に対応した$S,T$とその反転の$S^\dagger, T^\dagger$が実装されています.
$$ S\ket{x}= \left( \begin{array}{rr} 1 & 0 \\ 0 & i \\ \end{array} \right) \left( \begin{array}{r} a\\ b\\ \end{array} \right) =a\ket{0}+ib\ket{1} $$ $$ T\ket{x}= \left( \begin{array}{rr} 1 & 0 \\ 0 & exp(i\frac{\pi}{4}) \\ \end{array} \right) \left( \begin{array}{r} a\\ b\\ \end{array} \right) =a\ket{0}+exp(i\frac{\pi}{4})b\ket{1} $$
位相シフト演算$S^\dagger$と$T^\dagger$は, 元の$S$,$T$シフト演算の逆向きの回転になっています. よって, $SS^\dagger=I$, $TT^\dagger=I$となっています.

CNOTゲート
$$ CNOT^{(c,t)}≡ \left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{array} \right) $$
CNOT(controll-NOT)ゲートは, 2つの量子をもつれさせるゲートです. 今までのゲートが単一量子ビットの演算子(素子)だったのに対し, CNOTゲートは2量子ビットを必要とします. 基本的にはビット反転演算子Xを実行することができるゲートですが, この時別の量子ビットによって制御されていることが特徴です. NOT演算子(Xゲート)を制御することから, 制御NOTゲートとも呼ばれます.
CNOTゲートの実行には, 制御(controll)量子ビット$\ket{c}$と標的(target)量子ビット$\ket{t}$の二つが必要です. そして, 制御量子ビットが$\ket{0}$ならば何もせず, $\ket{1}$ならばXゲート(ビット反転)を実行します.
$$ CNOT\ket{00}=\ket{00} CNOT\ket{01}=\ket{01} $$ $$ CNOT\ket{10}=\ket{11} CNOT\ket{11}=\ket{10} $$
量子回路上では以下のように表現します. 十字になっているのが標的量子ビットで, 小さな塗りつぶされた丸が制御量子ビットです.

ここで, 先ほどの量子もつれの説明ででてきたBell pairの一つ,$\ket{Φ^+}$を生成してみましょう. Bell pairは,アダマールゲートとCNOTゲートを使えばすぐに生成できます.
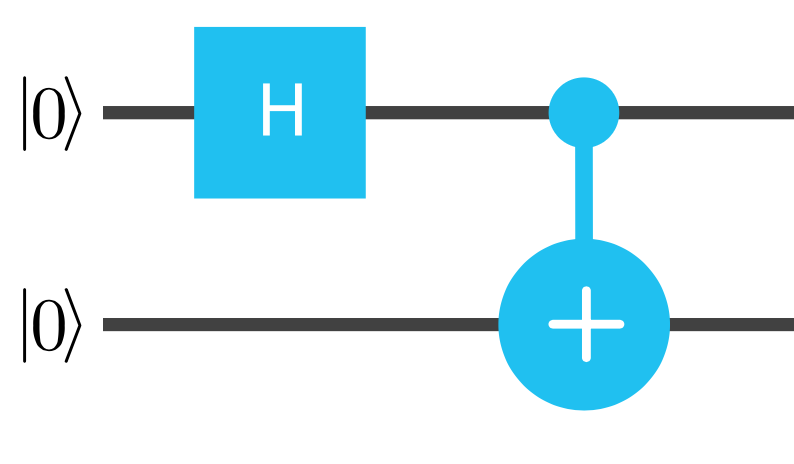
この時,二つの量子ビットはどのような行列の式で表現できるのでしょうか. 答えは, 一つの量子ビットは当然アダマールを適用するとして, もう一つの何もしない量子ビットに対しては,「何もしない」量子ゲートを適用したことにすればいいのです.「何もしない」量子ゲートは, 最初に説明したゲート, 恒等演算子(Id)のことでした. それを元に最初の段階の操作を式にすると以下のようになります.
- 第1量子ビット $ H\ket{0}=\frac{1}{\sqrt{2}} \left( \begin{array}{r} 1 \\ 1 \\ \end{array} \right) $
- 第2量子ビット $I\ket{0}=\ket{0}$
ここで, 二つの量子に別の量子ゲートを適用した場合, 操作をテンソル積を用いることでひとつの式にまとめることができます.(このためにわざわざ「何もしない」操作の式を立てたのです.)このまとめたテンソル積を, クロネッカー積と呼称します.
$$H\otimes I$$ $$=\frac{1}{\sqrt{2}}\left( \begin{array}{rr} 1 & 1 \\ 1 & -1 \\ \end{array} \right)\otimes\left( \begin{array}{rr} 1 & 0 \\ 0 & 1 \\ \end{array} \right) $$ $$=\frac{1}{\sqrt{2}}\left( \begin{array}{rr} 1\left( \begin{array}{rr} 1 & 0 \\ 0 & 1 \\ \end{array} \right) & 1\left( \begin{array}{rr} 1 & 0 \\ 0 & 1 \\ \end{array} \right) \\ 1\left( \begin{array}{rr} 1 & 0 \\ 0 & 1 \\ \end{array} \right) & -1\left( \begin{array}{rr} 1 & 0 \\ 0 & 1 \\ \end{array} \right) \\ \end{array} \right) $$ $$ =\frac{1}{\sqrt{2}}\left( \begin{array}{rrrr} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & -1& 0 \\ 0 & 1 & 0 & -1 \\ \end{array} \right) $$
ここまでくれば, あとはCNOTを適用するだけです.
観測
今まで説明してきたように, 量子ビットは重ね合わせやもつれの状態にすることが可能ですが, 量子ビットを観測すると状態が確定し, 重ね合わせや量子もつれは壊れてしまい, 古典ビットになります. 観測は以下のようなアイコンで表現します.
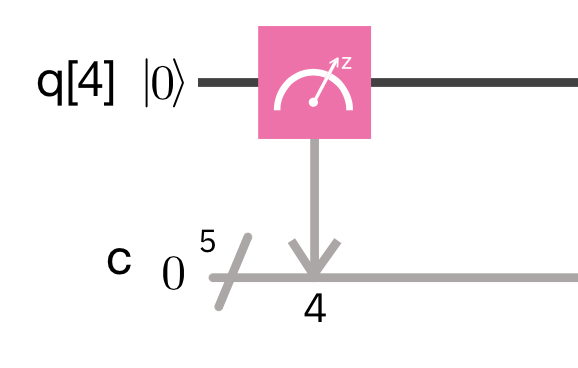
この図では, 第四量子ビットを測定し, 値(古典ビット)が得られるということを示しています.
IBM Qの使い方
IBMはクラウド上に誰でも無料で動かせる量子コンピュータを「IBM Quantum Experience」として公開しています. この量子コンピュータの本体はIBMのニューヨークの研究施設にあり, 利用者が命令を送るたびに実際に超電導回路で量子ビットを生成, 操作してくれます.

現在すぐに誰でも動かせる量子コンピュータは, IBM qx2, qx4, qx5の3種類です. これらが扱うことのできる量子ビットは,それぞれ5,5,17量子ビットです. qx5のみBeta版で,webサイト上のGUI(グラフィカルユーザインターフェース)に対応していないので今回は説明を省きます. qx2,qx4に関してはGUIが実装されており, 量子回路のグラフィックをいじることで量子コンピュータに行って欲しい命令を伝えることができます.

ただし, 量子コンピュータで量子もつれを生成するのには少し制限があります. 例えば, IBM qx4の設定を見ると以下のような図が表示されています.
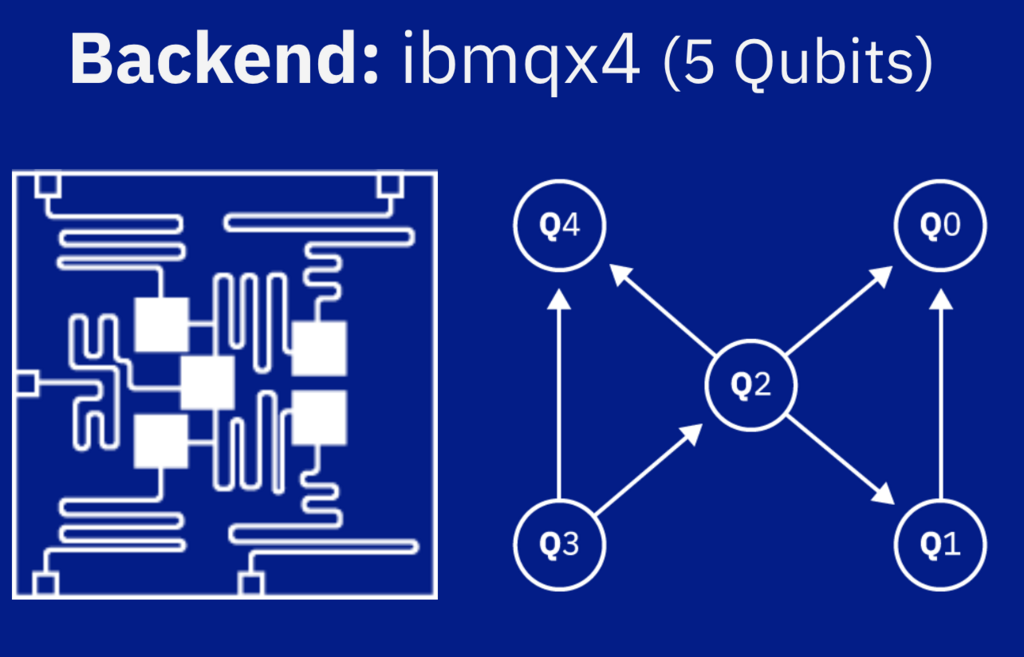
この図は, トポロジーと呼ばれるもので, 量子もつれ(CNOTゲート)に関する制限が書かれています. 読み方としては, 丸に囲まれたQ0からQ4が使用可能な量子ビットを表しています. 先ほど述べたようにqx4は5量子ビット使用可能なので, Q0,1,2,3,4の5つが表示されています. 各矢印は, 量子もつれ状態を生成可能(CNOTゲートを使用可能)であることを示しています. 矢印の方向は,コントロール量子ビット→ターゲット量子ビットになっています. なので, 例えばQ2の量子ビットは, CNOTゲートを用いるとき, Q3をコントロール量子ビットとしてターゲット量子ビットになることができ, また自身をコントロール量子ビットとしてQ0,1,4をターゲット量子ビットとすることができます.
IBMQはZ測定のみに対応していますが,ブロッホ球の回転操作を行うことによってX測定,Y測定に近い測定を行うことができます.これは,以下のような量子回路で実行できます. ただし,それぞれの操作によるノイズの発生があるので, より厳密な議論では注意が必要です.
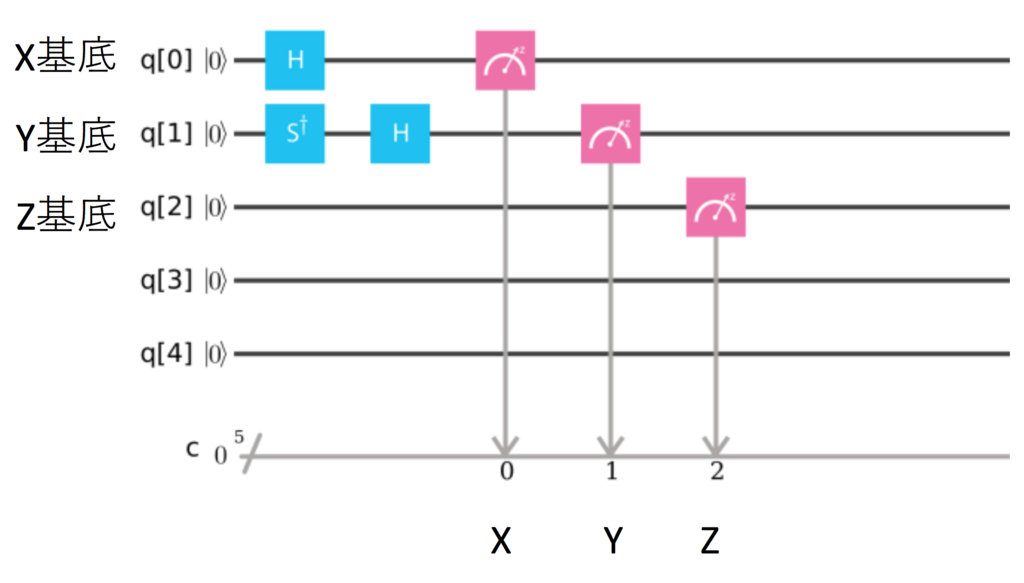
IBM Qを動かしてみる
実際にIBM qx4で動かしてみましょう. 現在の量子コンピュータでは計算を行うごとにノイズが発生しますが, それがどれだけ計算に影響を与えているか知ることができます. ノイズは, 量子ビットが物理的に存在するにあたって完全に閉じた系にすることが難しいことに起因しています. (量子コンピュータ外部からの振動や電磁波, 観測機器の故障や精度限界など様々な要因が考えられます.)
IBM Qの操作
IBM Qは, 量子回路の読み方がわかれば, 極めて簡単に量子ビットを操作することができるようなGUIが実装されています. ここまでの説明で量子回路の基礎は抑えたので, 早速動かしてみましょう.
まず, https://www.research.ibm.com/ibm-q/をwebブラウザで開いてください. すると以下のような画面が出てきます.
開けたら, 右側のExperimentに入り,"Start experimenting with a quantum computer"をクリックして開いてください. 次に, ページの右上にある"Sign In"をクリックしてください.メールアドレスを登録するか,IBM Id, Linkedin, Github, Google, Twitterなどのアカウントでログインができます.
Sign inするとCommunityのForumが表示されるので, 右上のメニューの"composer"を選択してください. 先ほど少し紹介したトポロジーが表示されるので下に行くと, 楽譜のようなものがあります. これが量子回路になっており, 右側に見える量子ゲートをマウスでドラッグ&ドロップすることで行いたい操作を設定できます. なお, 楽譜に似ているのでこの量子回路を"Composer"と称することがあります.
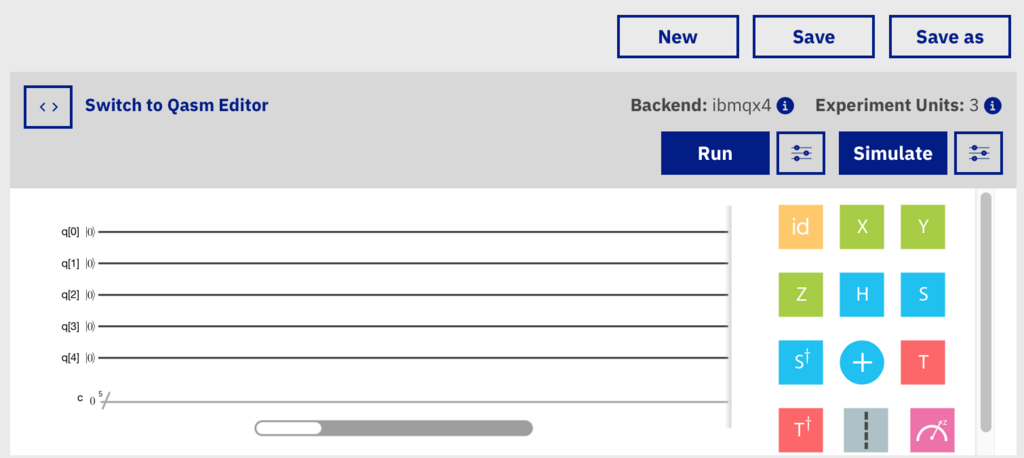
実行したい回路の作成が終わったら, 回路の右上のRunかSimulateをクリックしましょう.
Runを押すと実際の量子コンピュータを動かすことができ, Simulateをクリックすると, 古典コンピュータで量子コンピュータをシミュレートしたものを動かすことができます. 古典コンピュータによるシミュレータは, 実際の量子コンピュータと違ってノイズがほぼ全くない理想的な状態の計算を行うことができます(このことをフィデリティがほぼ1である、と呼称します). なお,現状の技術では量子ビット数が非常に少ないので古典コンピュータによるシミュレートが可能ですが, 今後量子ビット数が増えるにつれ, 古典コンピュータによるシミュレートが不可能になる(処理が追いつかなくなる)ことが明確に予測されています.
"Run"すると, 数時間から数日ほどしてから計算結果(量子の観測結果)がメールで届きます. ただし, すでに同じ回路を実行した人がいた場合, 過去の観測データを待たずに見ることもできます.また, 右上の”save”から自分の作った量子回路を保存することができます.
最近のニュース
IBMは, 2017年11月, 20量子ビット量子コンピュータの作成に成功したと発表しました. (12/15に利用開始)また、それを活用した50量子ビットのチップのプロトタイプも完成しているようです. 20量子ビットのものは, IBMQネットワークのメンバー(慶應義塾など)や一部企業はクラウド利用可能です. 20量子ビットのものはトポロジーが公開されていますが, 双方向のトポロジーになっており, 大変利便性が向上していると言えるでしょう.
@IBMResearch 20 qubit device is active online. Some very nice T1s and decent T2s, and I guess some tradeoff for readout fidelity (69%-94%) https://t.co/0BTJ6KsjnR #QuantumComputing pic.twitter.com/iDioTyba45
— Zlatko Minev (@zlatko_minev) 2017年12月14日
最後に
最後まで読んで頂き, ありがとうございました. ご意見, ご指摘などございましたらお気軽にツイッター(@shin_tsujido)までご連絡下さい.
|つじしん〉 (@shin_tsujido) | Twitter
今回は誌面の都合もあり, 量子回路を用いたアルゴリズムなどを紹介することはできませんでしたが, 次回以降アップデートしていきたいと思っております. 【12/23追記】 トポロジーのことをトモグラフィーと誤記していたため修正。 【12/25追記】 アダマールゲート、位相シフトゲートの式に符号の欠落が見られたため修正